"Gases ultrafríos de Bose y dipolares de fermi: un estudio cuántico de Monte Carlo"

El objeto de estudio de esta tesis son los sistemas dipolares en el régimen cuántico degenerado. Usualmente, tratar con sistemas de muchos cuerpos y para evaluar sus propiedades requiere ser capaz de resolver la ecuación de Schrödinger. En el presente estudio, empleamos diferentes métodos de Monte Carlo, que permiten encontrar soluciones numéricas de forma estocásticas. La primera y más simple de estas técnicas es el método Variational Monte Carlo (VMC), que da una solución variacional. Una mejora sobre lo anterior consiste en emplear el método  Diffusion Monte Carlo (DMC) que permite obtener soluciones exactas para el estado fundamental del sistema (cuando se estudian sistemas bosónicos). Continuamos presentando dos métodos que se basan en el formalismo Feynman de la mecánica cuántica: Path Integral Monte Carlo (PIMC) y Path Integral Ground State (PIGS), que proporcionan soluciones exactas para el problema bosónico a temperatura finita y en el límite de temperatura cero respectivamente. Para trabajar con sistemas fermionicos, el algoritmo DMC tiene que ser modificado según la prescripción Fixed-Node para evitar el problema del signo. Al hacerlo, los resultados obtenidos con DMC se corresponden a soluciones variacionales a la energía.

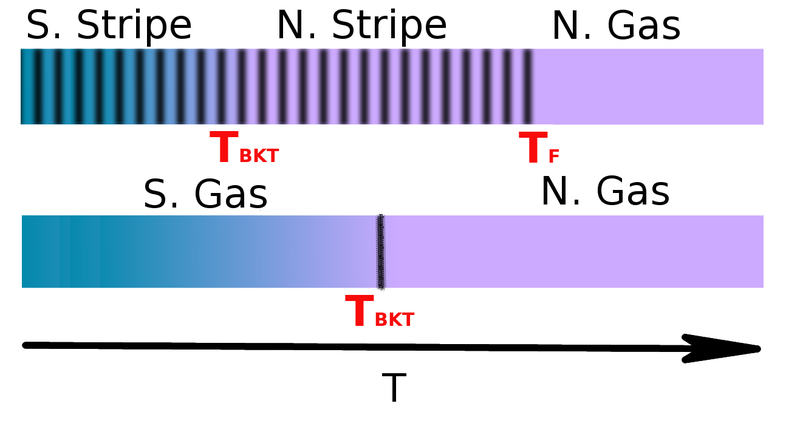
Primero estudiamos las propiedades superfluidas de un sistema de bosones dipolares completamente polarizados y en el que el movimiento de los dipolos está restringido al plano. También consideramos que los momentos dipolares forman un cierto ángulo con el eje perpendicular al plano, lo que permite introducir anisotropía en el sistema. El diagrama de fases a temperatura cero de este sistema revela la existencia de tres fases diferentes: gas, stripe y sólido. Aquí nos centramos en la caracterización de las propiedades superfluidas en ese diagrama de fases. Nuestros cálculos permiten abordar la cuestión de si la fase stripe de este sistema podría ser un candidato para el supersólido: un sistema en el que dos simetrías U (1) se rompen simultáneamente, permitiendo al sistema exhibir orden espacial de largo alcance y a la vez ser superfluido. Mediante el empleo de DMC y PIGS, evaluamos la fracción superfluida y el condensado, tanto en las fases de gas como en el stripe. Este estudio se completa con la extensión a temperatura finita, donde el uso de PIMC permite caracterizar la transición superfluida y obtener la temperatura crítica a la que ésta ocurre en las fases gas y stripe. Finalmente, por comparación directa con las predicciones Líquido de Luttinger, mostramos explícitamente que la fase de stripe no puede describirse como un conjunto de sistemas 1D aislados.

Después, estudiamos el sistema dipolar fermiónico en dos dimensiones, enfocándonos en el caso en que todos los dipolos están polarizados a lo largo de la dirección que es perpendicular al plano que contiene su movimiento. Calculamos la ecuación de estado del sistema en un amplio rango de parámetros de interacción: a baja densidad, la comparación de nuestro modelo dipolar con uno de discos duros permite determinar el régimen de universalidad, mientras que a densidades más altas (antes de la cristalización), discutimos la posibilidad de una fase polarizada como el estado fundamental del sistema (ferromagnetismo itinerante). El polaron fermiónico dipolar, correspondiente al límite de impurezas ultradiluídas en un baño fermiónico también es estudiado, determinando el régimen de universalidad y los límites de validez de la aproximación de cuasi-partícula.

Finalmente, la formación de gotas dipolares ultradiluídas es estudiada. Nuestros resultados están en acuerdo con medidas experimentales con átomos de disprosio. Por otro lado, la evaluación de las diferencias entre éstos y la predicción dada por la ecuación de Gross-Pitaevskii extendida, permite evaluar los límites de la aproximación mean-field para este problema.